Advanced Pythagorean Theorem Calculator
Calculate triangle sides using the Pythagorean theorem, explore geometric proofs, and discover real-world applications
Calculation Mode
Triangle Dimensions
Calculation Results
Triangle Visualization
Common Pythagorean Triples
Real-world Applications
Calculation History
Why Choose Our Pythagorean Theorem Calculator?
Multiple Calculation Modes
Go beyond finding the hypotenuse. Easily calculate a missing leg or verify if three sides form a valid right triangle.
Interactive Visualizations
Don't just see the numbers—understand the geometry. Our tool provides visual proofs of the theorem, including animated diagrams.
Step-by-Step Solutions
Choose the "Step-by-Step" mode to see a detailed breakdown of the calculation, perfect for students and teachers.
Real-World Applications
Explore how the theorem is used in construction, navigation, and computer graphics with our interactive real-world examples.
Explore Pythagorean Triples
Discover and load common, primitive, and special Pythagorean triples to quickly test and understand these unique number sets.
Calculation History
Keep track of your work. The tool automatically saves your recent calculations for easy review and reference.
Pythagorean Theorem Calculator: Your Easy Way to Solve Right Triangles
Understanding and solving right triangles has never been easier. Thanks to the Pythagorean Theorem Calculator, you can quickly find missing sides, angles, perimeter, or even verify the correctness of your triangle — without needing to do manual math. Whether you’re a student, an engineer, or someone dealing with construction measurements, this tool makes geometry fast and simple.
What Is the Pythagorean Theorem?
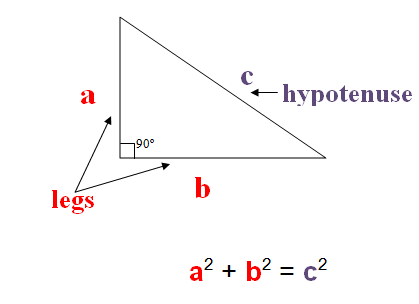
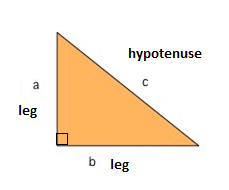
The Pythagorean Theorem is one of the most famous principles in mathematics. It applies specifically to right triangles — triangles with one 90° angle.
The theorem states:
a2+b2=c2a^2 + b^2 = c^2a2+b2=c2
a = one leg of the triangle
b = the other leg
c = the hypotenuse (the longest side opposite the right angle)
👉 In simple words, the square of the hypotenuse equals the sum of the squares of the two legs.
Example:
If one side is 3 and the other is 4, then:
32+42=9+16=253^2 + 4^2 = 9 + 16 = 2532+42=9+16=25
25=5\sqrt{25} = 525=5
So, c = 5
Why Use a Pythagorean Theorem Calculator?
Manually calculating triangle sides can be slow and prone to mistakes. A Pythagorean Theorem Calculator automates this process and gives instant, accurate results.
✅ Benefits:
Quickly find the missing side (a, b, or c).
Calculate angles and perimeter.
Works with feet, inches, decimals, or radicals.
Great for geometry homework, engineering, and real-world construction.
Supports multi-step and 3D calculations.
How to Calculate the Pythagorean Theorem
You can calculate the missing side of a triangle using:
To find c (hypotenuse):
c=a2+b2c = \sqrt{a^2 + b^2}c=a2+b2
To find a (one leg):
a=c2−b2a = \sqrt{c^2 – b^2}a=c2−b2
To find b (other leg):
b=c2−a2b = \sqrt{c^2 – a^2}b=c2−a2
👉 Or simply enter the values into the Pythagorean Theorem Calculator, and it does the rest for you in seconds.
Step-by-Step: How to Use the Calculator
Enter Known Values: Input the lengths of any two sides (a, b, or c).
Choose Units: Feet, inches, or decimal values.
Hit Calculate: The missing side and perimeter are automatically generated.
View Results: Instantly get the hypotenuse, missing leg, and angle measurements.
This makes solving triangles as easy as pressing a button.
Pythagorean Theorem Calculator Angle
Apart from finding side lengths, many users want to calculate angles too.
Using trigonometric functions:
sinθ=oppositehypotenuse\sin \theta = \frac{\text{opposite}}{\text{hypotenuse}}sinθ=hypotenuseopposite
cosθ=adjacenthypotenuse\cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}}cosθ=hypotenuseadjacent
tanθ=oppositeadjacent\tan \theta = \frac{\text{opposite}}{\text{adjacent}}tanθ=adjacentopposite
Our Pythagorean Theorem Calculator with angles gives angle results automatically — no need to memorize formulas.
Finding Missing Legs with the Calculator
If you know the hypotenuse and one leg, the calculator can find the missing leg.
Example:
If c = 10 and a = 6,
b=102−62=100−36=64=8b = \sqrt{10^2 – 6^2} = \sqrt{100 – 36} = \sqrt{64} = 8b=102−62=100−36=64=8
✅ Result: b = 8 units
This is why many people search “Pythagorean theorem calculator find b” or “find the missing leg length calculator” — because the tool solves it instantly.
Pythagorean Theorem Hypotenuse Calculator
Finding the hypotenuse is the most common use of this tool. Simply plug in a and b.
Example:
a = 9, b = 12
c=92+122=81+144=225=15c = \sqrt{9^2 + 12^2} = \sqrt{81 + 144} = \sqrt{225} = 15c=92+122=81+144=225=15
✅ Hypotenuse: 15
No more manual squaring or square rooting — the calculator does it for you.
Using the Calculator for Right Triangles
The Pythagorean theorem right triangle calculator works exclusively for right-angled triangles. If the triangle isn’t right-angled, the theorem doesn’t apply.
Features:
Handles integer, decimal, feet, and inches.
Supports fractions and radical forms.
Ideal for geometry students and builders.
Multi-Step and 3D Pythagorean Theorem Calculations
The multi-step Pythagorean theorem calculator can solve more advanced problems like:
Diagonal distances in 3D space
Construction site measurements
Complex shapes with multiple right triangles
3D version:
d=x2+y2+z2d = \sqrt{x^2 + y^2 + z^2}d=x2+y2+z2
How to Calculate Distance Using the Pythagorean Theorem
The theorem is widely used to calculate distance between two points.
For 2D:
d=(x2−x1)2+(y2−y1)2d = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}d=(x2−x1)2+(y2−y1)2
This is the same principle behind the distance formula taught in algebra and geometry.
Converse of the Pythagorean Theorem
Did you know you can also verify if a triangle is right-angled using the theorem?
If:
a2+b2=c2a^2 + b^2 = c^2a2+b2=c2
then the triangle is right-angled.
This is why the converse of the Pythagorean theorem calculator is also popular — especially among students.
Pythagorean Theorem Calculator in Feet and Inches
Sometimes measurements are not in decimals but feet and inches (especially in construction).
Example:
a = 5 ft 6 in, b = 7 ft 3 in
The calculator automatically converts and computes the result.
It’s perfect for:
Carpenters
Architects
DIY projects
Pythagorean Theorem Calculator with Radical Form
For math students, the radical form gives exact values rather than decimals.
Example:
a = 8, b = 15
c=82+152=64+225=289=17c = \sqrt{8^2 + 15^2} = \sqrt{64 + 225} = \sqrt{289} = 17c=82+152=64+225=289=17
If the answer isn’t a perfect square, the calculator can simplify radicals too — making it an excellent learning tool.
Applications of the Pythagorean Theorem
Mathematics & Geometry – solving triangles, trigonometry
Architecture – building designs, structural layouts
Navigation – shortest distance calculations
Physics & Engineering – forces and vectors
Computer Graphics – distances in 2D and 3D space
Astronomy – calculating distances in space
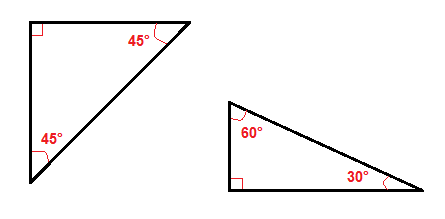
Pythagorean Theorem Calculator for Isosceles and Special Triangles
Even though the theorem applies only to right triangles, you can use it to find missing lengths in isosceles right triangles and special 30-60-90 or 45-45-90 triangles.
👉 For example, in a 45-45-90 triangle:
c=a×2c = a \times \sqrt{2}c=a×2
The calculator handles these special cases automatically.
How to Do the Pythagorean Theorem on a Calculator
If you want to calculate manually:
Square the lengths of a and b.
Add the results.
Take the square root of the sum.
But why do it manually when the Pythagorean theorem calculator can do it instantly?
Best Features of a Pythagorean Theorem Calculator
🧮 Supports a, b, and c calculations
📐 Finds angles and perimeter
📏 Works with different units
📊 Handles fractions, radicals, 3D
📲 Free and easy to use online
✅ Provides step-by-step solutions
Tips for Using the Calculator Effectively
Always enter accurate values.
Double-check units (feet, inches, or decimals).
Use the “show work” option to learn the steps.
Explore 3D and angle modes for complex problems.
Save results for reference.
Pythagorean Theorem Calculator vs Manual Calculation
| Feature | Manual Calculation | Online Calculator |
|---|---|---|
| Speed | Slow | Fast ⏱️ |
| Accuracy | Depends on user | 100% |
| Step-by-step solution | Manual | Auto-generated |
| Multi-step / 3D support | Complex | Easy |
| Angle calculation | Hard | One-click |
Why Students Love the Pythagorean Theorem Calculator
No more memorizing formulas
Instant results for homework
Learn while you calculate
Perfect for algebra, trigonometry & geometry
Why Professionals Use It
Builders use it for roofing, flooring, and layouts.
Engineers use it to measure angles and distances.
Designers use it to ensure perfect right angles.
Surveyors use it to measure land accurately.
Building Trust: Why Accuracy Matters
Geometry is all about precision. A small error in measuring can lead to a big structural issue in real life. That’s why using a reliable Pythagorean theorem calculator ensures:
✅ Accurate outputs
✅ Secure computations
✅ Trustworthy measurements
Final Thoughts: Master Geometry with Ease
The Pythagorean Theorem Calculator turns complex geometry into something anyone can solve.
Whether you’re a student trying to solve homework problems or a professional working on real-world projects, this tool makes calculations fast, easy, and accurate.
FAQs
Q1: What is a Pythagorean Theorem Calculator?
A Pythagorean theorem calculator is an online tool that quickly solves for missing sides or angles of a right triangle using the Pythagorean theorem.
Q2: How do I find the hypotenuse using the calculator?
Just enter values for a and b, then hit “Calculate.” The tool will display c instantly.
Q3: Can the calculator find angles too?
Yes! It can calculate angles using sine, cosine, and tangent functions.
Q4: Is the Pythagorean theorem only for right triangles?
Yes, it only applies when one angle is 90°.
Q5: Can it handle feet and inches?
Absolutely. The calculator works with various units including feet, inches, and decimals.
Q6: What if I know the hypotenuse and one leg?
The calculator can solve for the missing leg instantly using the rearranged formula.
Q7: Can I use it for 3D problems?
Yes. The 3D mode calculates diagonal distances in three dimensions.
Q8: Is this tool free to use?
Yes, it’s completely free and online.
Q9: Can it solve word problems too?
Yes. If you can convert the problem into numbers (a, b, c), the calculator will solve it.
Q10: Is the calculator accurate for professional use?
Yes, the results are mathematically precise and widely used in professional fields.
Meet the Author

Anam Ahsan
Anam Ahsan, SEO expert & web strategist, helps users access powerful online tools to boost productivity, accuracy, and digital growth.
Anam Ahsan is the founder of TryToolsBox.com, a platform dedicated to providing free, reliable, and easy-to-use online tools that help individuals, writers, students, and professionals enhance their productivity and accuracy.
